Split Streams and Circularity
Introduction
In order to facilitate the modeling of real life projects, PetroVR uses non-trivial routing algorithms that support capacity constraints, downtimes, separation of fluid phases and components, ensured rates and proportional routing. In view of these many possibilities, split streams are especially challenging as they usually create flowing arrangements whose routings are hard to compute. More precisely, splits streams make it easy to create circuits that cannot be efficiently solved with accuracy. This section explains the problem posed by split streams and how PetroVR addresses them with a trade-off between computational performance and accuracy.
Let's start with a simple case where a facility receives fluids from two different sources:
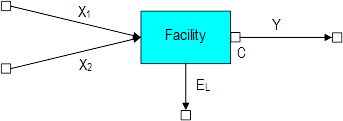
Because of the capacity constraints, if the sum X1 + X2 surpasses certain limits, then a part of them will be sent back to the sources instead of going through the facility. Two excess points can be easily identified in the diagram. The first one is the local excess EL associated to the capacity C. The other one is the downstream excess ED associated to the amount sent back to the facility after routing Y = min(C, X1 + X2). In the routing process the total excess E = EL + ED has to be returned to the sources to honor both local and downstream constraints.
With the proportional choke strategy (see Well Chokes), the amount returned to each source is proportional to the amount that source contributed to the input. For instance, if X1 is twice X2 then its source will be sent back twice the amount returned to the second source. The streams push with pressures that are proportional to their (instantaneous) rates.
Adding split streams
Now let's complicate the diagram by adding a split stream:
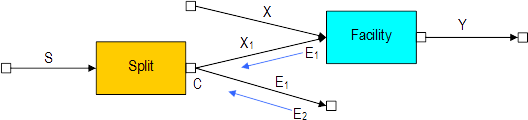
The behavior of the split is to send as much as possible through its first branch, reroute whatever is left to the second, and return the resulting excess back to the source.
This means that the first branch of the split will push with strength proportional to S (actually proportional to min(S, C) because of the local capacity constraint C).
The behavior of the split also implies that the excess E1 downstream the first branch will push through the second branch. That second branch will eventually cause some excess downstream E2 that will be sent back to the source of the split.
As we can see, in order to compute the routing we need to compute E1 and E2. However, let's point out that E2 depends on E1 since the amount sent down the second branch is precisely E1. As we will see in the next section this is the source of a circularity problem.
The circularity problem
Splits can create circularities like the one depicted below:
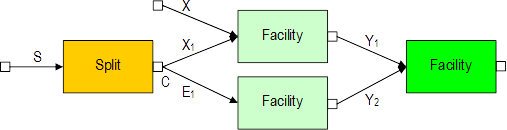
The cycle in the circuit produces circularity in the computation of the routing. As we saw in the previous section, the rate E1 in the second branch of the split is the excess on the first branch. In turn, the excess in the first branch depends on the excess in the Y1 branch of the last facility, which ultimately depends on E1.
Solving the circularity problem
The circularity problem happens in real-life projects, and there are basically two ways to address it. The first one consists in using an iterative algorithm that starting with rather arbitrary initial values for the unknowns is able to find a better estimate after a number of consecutive iterations. This approach has been discarded because it does not fit well in the way PetroVR performs the routing of fluids.
PetroVR attacks the problem by deferring the routing among the split branches by one day. In other words, the excess E1 of the first branch is not derived to the second branch today but tomorrow. Such deferment breaks the circularity because it avoids solving both flows simultaneously.
The trade-off between performance and accuracy
Several tests showed that the inaccuracy derived from the delay of 1 day introduced in our solution is minimal and correct for all practical purposes. Unfortunately, this solution impacts the performance. Usually the simulation does not step day by day; it jumps over periods of inactivity. The jumps allow the simulation to reach a performance which would otherwise be too slow.
The problem with jumps is that they impact the amount of inaccuracy derived from the delays. This inaccuracy is acceptable if it corresponds to a delay of 1 day. However, tests have shown that the inaccuracy derived from delays of several days (typically 30-60 days) is highly misleading.
Understanding the imbalance
The origin of the imbalance related to the long delays in the case of split streams resides in the fact that the excess E1 of the first branch is not immediately sent to the second branch. Instead, it is sent downstream after a given number of days. Because of this, the quantity E1 would not be contributed to the rate of any facility, as it is waiting in the pipe instead of flowing downstream. The imbalance would even out if we could assign the fluid in the pipe to some facility. In the end everything balances out. However, intermediary photos used to collect the history of the simulation along the reporting periods make the temporary imbalance apparent and misleading.
A fast solution to the circularity problem
Once the source of the imbalance as the amount of fluid waiting in the pipes has been identified, one possible solution that fits well with the PetroVR metaphor is to flush the pipes before taking the photo.
Flushing the pipes means that any fluid that is waiting for the next step to be sent through a connection is immediately sent instead. Since the reporting periods are comparatively few when compared to the total number of steps, the cost of flushing the pipes can be neglected.
After the flushing, all the pipes are empty and the system balances exactly. Note that the flushing is instantaneous, it doesn't take time (the timer does not change) and it takes no resources (the wells do not send their productions).
Warning
Despite its efficiency, this solution could produce some inaccuracy. The flush could contribute to the actual routing in a way that some capacity is not honored. That side effect is possible because the actual routing and the flush are done separately while in reality they occur at the same time.
